Verifying Refinement

Refinement and simulation

We say that system \(B\) refines system \(A\) if any step taken by \(B\) can be simulated by a sequence of steps by system \(A\) such that the observed effects are identical. As a toy example, consider the two state machines below. Machine \(A\) implements a one-bit counter and outputs \(\texttt{0}\) and \(\texttt{1}\) when in states \(0\) and \(1\) respectively. Machine \(B\) on the other hand implements a two-bit counter: also outputting \(\texttt{0}\) and \(\texttt{1}\) but now in states \(00\) and \(10\) respectively.

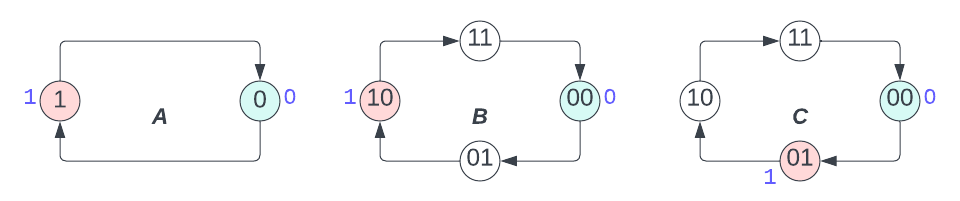
The machine \(A\) on the left is refined by the machine \(B\). This is illustrated with the following executions. Any execution of machine \(B\) cycles through its states generating the outputs \(\texttt{0}\) and \(\texttt{1}\) in the green and pink states respectively. But any such execution can be matched with an execution of \(A\), which also generates the same sequence of outputs (albeit in different states). The state coloring identifies a refinement relation: whatever happens in the green (pink) states in \(B\) also happens in the green (pink) states in \(A\).

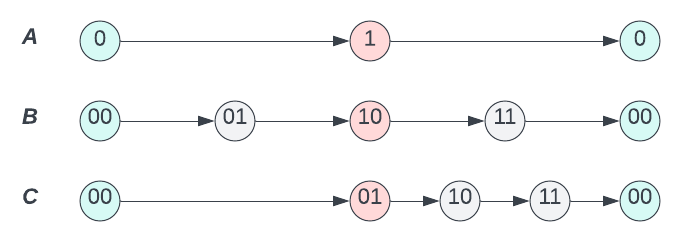
We observe that third machine \(C\) also refines \(A\) but in a different way: can you find the refinement relation in this case?

Refinement proofs in UCLID5

We can use the features in UCLID5 to specify and hence verify that one system refines another. Typically such a refinement proof takes the form of a following diagram:

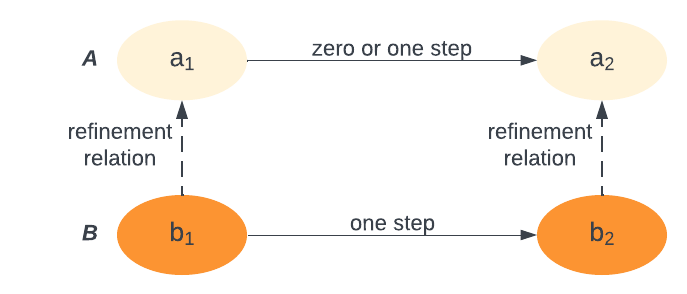
Here we want to prove that the system \(A\) (above) is refined by the system \(B\) (below). This requires us to define a refinement relation between states in the two systems as we saw earlier. The proof itself starts by assuming that two states, one each from \(A\) and \(B\), which satisfy the refinement relation. In our example these are \(a_1\) and \(b_1\) respectively.

Then system \(B\) is transitioned for one step, while \(A\) is transitioned for zero or one steps (also called a stuttering transition). Finally the proof checks that the states that result - \(a_2\) and \(b_2\) in our example - also satisfy the refinement relation. This check sets up an inductive proof that \(A\) simulates \(B\) - or \(B\) refines \(A\) as depicted in the figure below.

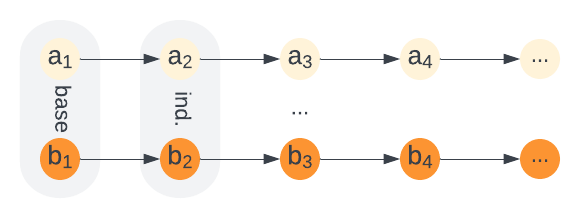
An example of refinement checking, the verification of a simple pipelined datapath, is illustrated in detail in the code here. Observe that in this example the spec module describes the system that simulates the one described by the impl module.